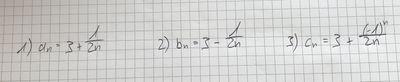Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Benutzer:PascalHänle/Folgen und Grenzwert: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 15: | Zeile 15: | ||
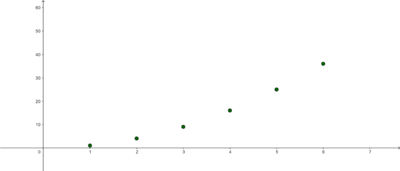
[[Datei:Folgen.jpg|rand|400x400px|3 verschiedene Folgen ]] | [[Datei:Folgen.jpg|rand|400x400px|3 verschiedene Folgen ]] | ||
'''b)''' Überprüfe Deine Vermutung mit Hilfe der Tabelle, indem Du in die Spalte der Platznummer wachsende | '''b)''' Überprüfe Deine Vermutung mit Hilfe der Tabelle, indem Du in die Spalte der Platznummer wachsende Zahlen einsetzt. {{Lösung versteckt|<iframe src="https://www.geogebra.org/classic/yxt2my2n?embed" width="500" height="800" allowfullscreen style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe>|Tabelle 1 anzeigen|Tabelle 1 verbergen}} | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
Version vom 7. September 2020, 15:10 Uhr
Folgen und Grenzwerte
Beim Spiel Mensch ärgere Dich nicht benötigt man eine 6 um mit dem ersten Männchen ins Spiel einzusteigen.
Aufgabe 1
a) Wie groß ist die Wahrscheinlichkeit, dass drei Würfe, vier Würfe, fünf Würfe, …, n Würfe genügen, um ins Spiel zu kommen. Stelle hierzu eine Folge in expliziter Schreibweise auf.
Aufgabe 2
Aufgabe 3
Fasse Deine Erkenntnis aus Aufgabe 1 und 2 zusammen und formuliere eine Eigenschaft für Folgen wie aus Aufgabe 1 und 2.