Zentrische Streckung/Vierstreckensatz/3.Station: Unterschied zwischen den Versionen
Main>Leonie Porzelt KKeine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
<div style="border: 2px solid #0000ff; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ff; background-color:#ffffff; padding:7px;"> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<math>\overline{ZA'} =</math> '''<math>\mid k\mid \cdot \overline{ZA}</math>''' <math>\mathit{und} | <math>\overline{ZA'} =</math> '''<math>\mid k\mid \cdot \overline{ZA}</math>''' <math>\mathit{und} </math> <math>\overline{A'B'} =</math> '''<math>\mid k\mid \cdot \overline{AB}</math>'''<br> | ||
Aufgelöst nach |k|:<br> | Aufgelöst nach |k|:<br> | ||
<math>\mid k\mid =</math> '''<math>{\overline{ZA'}\over\overline{ZA}}</math>''' <math>\mathit{und} | <math>\mid k\mid =</math> '''<math>{\overline{ZA'}\over\overline{ZA}}</math>''' <math>\mathit{und} </math> '''<math>\mid k\mid</math>''' <math>= {\overline{A'B'}\over\overline{AB}}</math><br> | ||
Gleichsetzen:<br> | Gleichsetzen:<br> | ||
<math>{\overline{ZA'}\over\overline{ZA}} = {\overline{A'B'}\over\overline{AB}}</math><br> | <math>{\overline{ZA'}\over\overline{ZA}} = {\overline{A'B'}\over\overline{AB}}</math><br> | ||
| Zeile 36: | Zeile 36: | ||
[[Bild:Porzelt_Panto-2.jpg|left]] | [[Bild:Porzelt_Panto-2.jpg|left]] | ||
<br> | <br> | ||
Dieser Satz sagt aus, dass sich die Streckenabschnitte auf den Parallelen wie die zugehörigen Streckenlängen (von Z ausgehend<br> | Dieser Satz sagt aus, dass sich die Streckenabschnitte auf den Parallelen wie die zugehörigen Streckenlängen (von Z ausgehend)<br> | ||
auf einer Geraden verhalten.<br> | auf einer Geraden verhalten.<br> | ||
</div> | </div> | ||
| Zeile 54: | Zeile 54: | ||
'''Panto hat natürlich versucht auf die Kletterwand zu klettern. Denkst du, er hat es geschafft? Wenn du es wissen willst,'''<br> | '''Panto hat natürlich versucht auf die Kletterwand zu klettern. Denkst du, er hat es geschafft? Wenn du es wissen willst,'''<br> | ||
'''dann lass es dir anzeigen!''' <br> | '''dann lass es dir anzeigen!''' <br> | ||
{{ | {{Lösung versteckt| | ||
[[Bild:Porzelt_4-Streckensatz-Kletterwand-Lösung.jpg]]|}} | [[Bild:Porzelt_4-Streckensatz-Kletterwand-Lösung.jpg]]|}} | ||
<br> | <br> | ||
<div align="left">[[Lernpfade/Zentrische Streckung/Vierstreckensatz/4.Station|<math>\Rightarrow</math> Weiter zur 4. Station: Zusammenfassung]]</div> | <div align="left">[[Lernpfade/Zentrische Streckung/Vierstreckensatz/4.Station|<math>\Rightarrow</math> Weiter zur 4. Station: Zusammenfassung]]</div> | ||
<br> | <br> | ||
<div align="left">[[Lernpfade/Zentrische Streckung/Vierstreckensatz/2.Station|<math>\Leftarrow</math> Zurück zur 2. Station: Erster Vierstreckensatz - Abschnittlösung]]</div> | <div align="left">[[Lernpfade/Zentrische Streckung/Vierstreckensatz/2.Station|<math>\Leftarrow</math> Zurück zur 2. Station: Erster Vierstreckensatz - Abschnittlösung]]</div> | ||
[[Kategorie:Keine Kategorie]] | |||
Aktuelle Version vom 23. April 2022, 16:02 Uhr
1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung
3. Station: Zweiter Vierstreckensatz
Früher wurden die Höhen von Pyramiden, Bäumen, Türmen usw. berechnet, indem man einen Stab lotrecht so aufstellte,
dass das Ende seines Schattens mit dem Ende des Schattens des Objektes zusammenfiel. Dabei wurde die Länge des Schattens
des Objektes und die Länge des Schattens vom Stab gemessen.
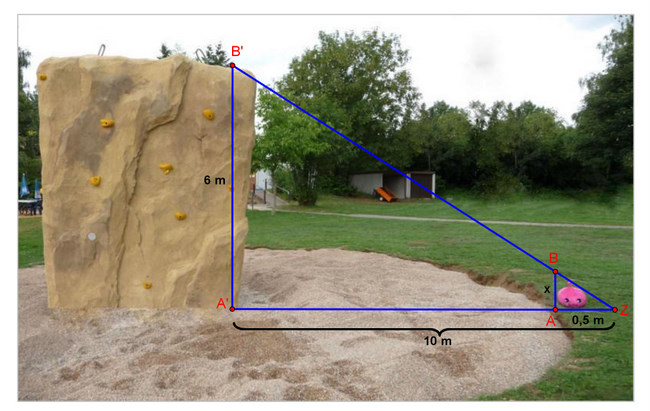
Wie du auf dem Bild sehen kannst, hat Panto einen Stab vergessen und sich selbst platziert. Panto weiß, dass die Kletterwand
6 m hoch ist, nur hat er mit zunehmendem Alter vergessen, wie groß er ist.
Hilf ihm, seine Größe herauszufinden:
Zunächst musst du wieder eine passende Formel zur Berechnung der gesuchten Strecke x herleiten! Setze wieder die richtige
Aussage in die passende Lücke ein:
Aufgelöst nach |k|:
Gleichsetzen:
Dieser Satz sagt aus, dass sich die Streckenabschnitte auf den Parallelen wie die zugehörigen Streckenlängen (von Z ausgehend)
auf einer Geraden verhalten.
Trage hier deine Lösung mit Angabe der Einheit (m) ein!
Umstellen, damit die gesuchte Länge links oben steht:
Berechne das Ergebnis mit dem Taschenrechner:
x = 0,3 m (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).
Panto hat natürlich versucht auf die Kletterwand zu klettern. Denkst du, er hat es geschafft? Wenn du es wissen willst,
dann lass es dir anzeigen!





