Sinus- und Kosinusfunktion/2.2 Kosinusfunktion: Unterschied zwischen den Versionen
K (Kilian Schoeller verschob die Seite Mathematik-digital/Sinus- und Kosinusfunktion/2.2 Kosinusfunktion nach Sinus- und Kosinusfunktion/2.2 Kosinusfunktion) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
==Station 2: Sinusfunktion und Kosinusfunktion== | ==Station 2: Sinusfunktion und Kosinusfunktion== | ||
==2.2 Kosinusfunktion== | ===2.2 Kosinusfunktion=== | ||
{{ | {{Box|1=Üben|2= | ||
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). | Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). | ||
Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. | Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. | ||
Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen. | |||
< | <ggb_applet id="AtX3XWby" width="100%" height="450" border="888888" /> | ||
|3=Üben}} | |||
Halte deine Erkenntnisse nun schriftlich fest: | Halte deine Erkenntnisse nun schriftlich fest: | ||
{{ | |||
{{Box|Aufgabe - 2.2 Kosinusfunktion|Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.|Arbeitsmethode}} | |||
<br> | <br> | ||
{{Frage| | {{Box-spezial | ||
Überlege: Was könnte das bedeuten? | |Titel= Frage | ||
|Inhalt= Überlege: Was könnte das bedeuten? | |||
<math> cos(-\frac{\pi}{2}) </math> oder <math> cos(410^\circ) </math> | |||
Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft. | Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft. | ||
|Farbe= #cccccc | |||
|Icon= {{Icon question}} | |||
}} | }} | ||
{| | {{Lösung versteckt|1=Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn. | ||
[[Datei:Negativer Winkel.png|links|x200px|Negativer Winkel]] | |||
Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn. | |2=Lösung 'Negativer Winkel' anzeigen|3=Lösung verbergen}} | ||
[[Datei:Negativer Winkel.png|links|x200px|Negativer Winkel]] | |||
| | {{Lösung versteckt|1= | ||
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder <math>3\pi</math> | Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder <math>3\pi</math> | ||
[[Datei:Winkel größer 360°.png|links|x200px|Winkel größer 360°]] | [[Datei:Winkel größer 360°.png|links|x200px|Winkel größer 360°]] | ||
|2=Lösung 'Großer Winkel' anzeigen|3=Lösung verbergen}} | |||
|} | |||
<br> | <br> | ||
Teste, ob du alles verstanden hast! | Teste, ob du alles verstanden hast! | ||
{{ | |||
{{Box|1=Üben|2='''Kosinusfunktion verstanden?''' | |||
<br> | <br> | ||
{{LearningApp|app=p12tazmca17|width=100%|height=400px}} | |||
}} | |||
|3=Üben}} | |||
'''So, nun hast du alles wiederholt, was wir schon besprochen haben. Jetzt kommt was neues. Du darfst gespannt sein! :) | '''So, nun hast du alles wiederholt, was wir schon besprochen haben. Jetzt kommt was neues. Du darfst gespannt sein! :) | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| Zeile 61: | Zeile 55: | ||
|} | |} | ||
---- | |||
{{Lernpfad Sinus- und Kosinusfunktion}} | |||
{{Lernpfad Sinus und Kosinusfunktion}} | |||
Version vom 17. August 2018, 13:22 Uhr
Station 2: Sinusfunktion und Kosinusfunktion
2.2 Kosinusfunktion
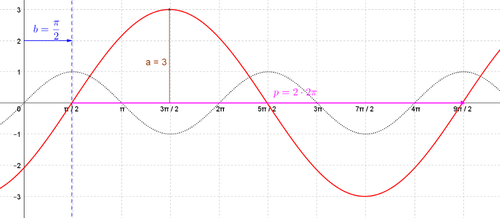
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen.

Halte deine Erkenntnisse nun schriftlich fest:
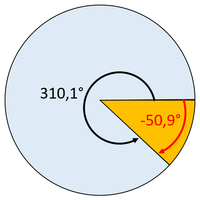
Ein negativer Winkel bedeutet, dass man den Winkel nicht im Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn.
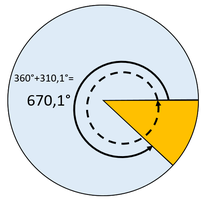
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder
Teste, ob du alles verstanden hast!
Kosinusfunktion verstanden?
So, nun hast du alles wiederholt, was wir schon besprochen haben. Jetzt kommt was neues. Du darfst gespannt sein! :)
| Hier geht es weiter... |