Prozente und Prozentrechnung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 36: | Zeile 36: | ||
TEST | TEST | ||
<iframe src="https://www.geogebra.org/classic/rytqqtnq?embed" width="800" height="600" allowfullscreen style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe> | <iframe src="https://www.geogebra.org/classic/rytqqtnq?embed" width="800" height="600" allowfullscreen="" style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe> | ||
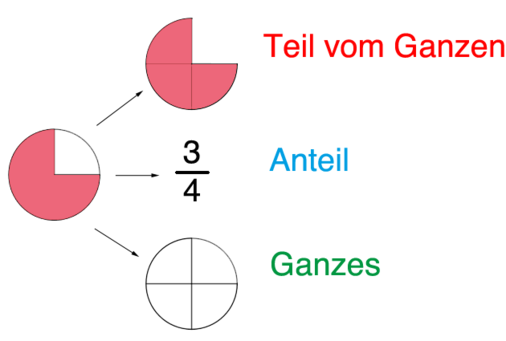
Du kannst im nachfolgenden Lückentext überprüfen, ob du nun weißt, was <span style="color: red">Bruchteil </span>, <span style="color: green">Anteil </span> und <span style="color: blue">Ganzes </span> sind. | |||
<div class="lueckentext-quiz"> | |||
Wenn du einen Bruch in einer Sachsituation gegeben hast, dann kannst du bei dem Bruch immer Bruchteil, Anteil und '''Ganzes''' betrachten. Das Ganze stellt den '''Ausgangspunkt''' dar, auf welchen sich der '''Bruchteil''' und der Anteil beziehen. Bei Brüchen wird meist nur ein gewisser '''Teil''' des Ganzen betrachtet. Dabei handelt es sich um den Bruchteil. Das Verhältnis zwischen Bruchteil und Ganzem spiegelt sich im '''Anteil''' wieder. | |||
</div> | |||
Version vom 21. August 2021, 14:25 Uhr
Herzlich willkommen im Lernpfad Prozente und Prozentrechnung!
Dieser Lernpfad soll dir dabei helfen, dein Wissen aus der Bruchrechnung auf die Prozentrechnung zu übertragen und deine Vorstellung von Prozenten auf- bzw. auszubauen.
Das Schöne daran ist, dass du vieles von dem, was du bereits aus der Bruchrechnung kennst, hier direkt anwenden kannst.
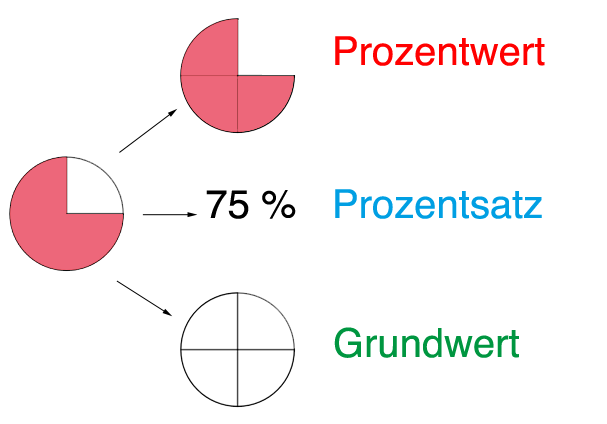
Der Begriff "Prozent" heißt dabei nichts anderes als "von Hundert". Du hast es also im Prinzip mit nichts anderem zu tun, als einem Bruch, dessen Nenner immer 100 ist. Es gibt also keinen Grund, vor der Prozentrechnung Angst zu haben!
Also: Leg los!
Wiederholung: Bruchteil, Anteil und Ganzes
In diesem Beispiel schauen wir uns noch einmal drei Viertel eines Kreises an.
TEST
Du kannst im nachfolgenden Lückentext überprüfen, ob du nun weißt, was Bruchteil , Anteil und Ganzes sind.
Wenn du einen Bruch in einer Sachsituation gegeben hast, dann kannst du bei dem Bruch immer Bruchteil, Anteil und Ganzes betrachten. Das Ganze stellt den Ausgangspunkt dar, auf welchen sich der Bruchteil und der Anteil beziehen. Bei Brüchen wird meist nur ein gewisser Teil des Ganzen betrachtet. Dabei handelt es sich um den Bruchteil. Das Verhältnis zwischen Bruchteil und Ganzem spiegelt sich im Anteil wieder.