Logarithmusfunktion

Lernpfad zur Logarithmusfunktion

Info zur Bearbeitung

Bearbeitet die folgenden Aufgaben zur Logarithmusfunktion. Was ihr jeweils zu tun habt steht in der Aufgabenstellung. Teilweise gibt es Buttons mit "Tipp" und "Lösung". Wenn ihr auf diese klickt, öffnet sich entsprechend ein Tipp zur Bearbeitung oder die Lösung der Aufgabe.

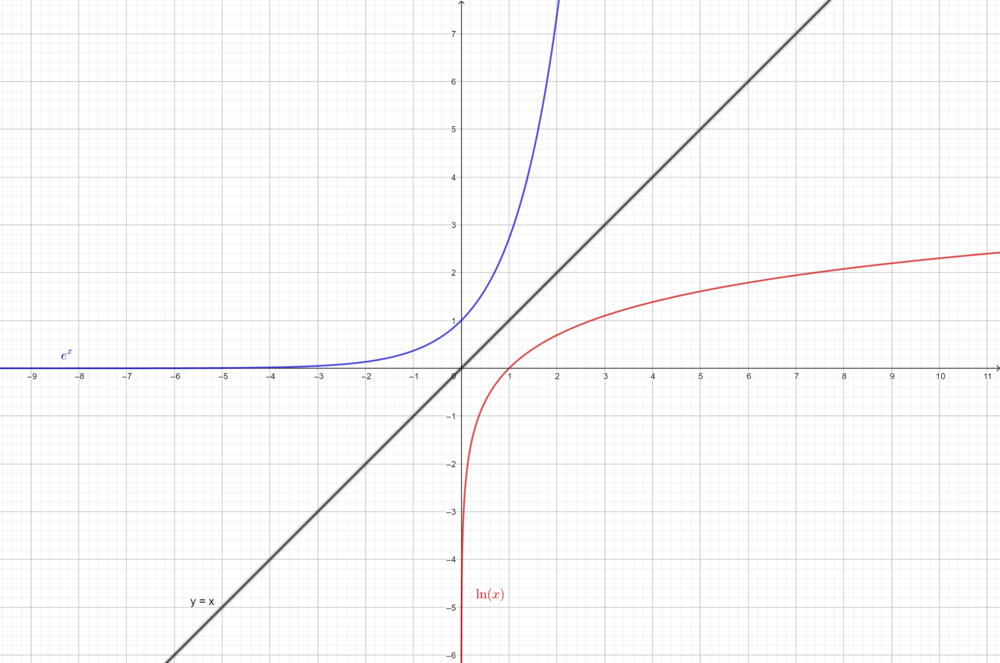
1. Erkundung der Logarithmusfunktion

(Sollte euch das Applet nicht angezeigt werden hilft es i.d.R. ein paar mal die Seite zu aktualisieren. Sollte es dann immer noch nicht gehen, dann öffne GeoGebra separat auf deinem PC (o.ä.) und gib die Funktion $f(x)=a\cdot ln(bx+c)+d$ ein. Es müssten sich dann automatisch Schieberegler für die einzelnen Variablen erstellen, die du dann verstellen kannst.)

a) Setzt $a$ und $b$ auf $1$ und $c$ und $d$ auf $0$. Zoomt in dem GeoGebra-Applet ganz nah an die y-Achse heran und folgt dem Verlauf des Graphen. Was fällt euch auf?

b) Zoomt wieder raus. Probiert die verschiedenen Schieberegler aus. Verändert dabei immer nur einen und notiert euch welchen Einfluss die jeweilige Änderung auf den Funktionsgraphen hat.

2. Nice to know!

Was ist der Logarithmus überhaupt?

3. Die Ableitung des natürlichen Logarithmus

Auch die Ableitung von $\bar{f}(x)=ln(x)$ kann mit Hilfe der obigen Ableitungsregel für Umkehrfunktionen berechnet werden.

Aufgabe: Leite mit Hilfe dieser Ableitungsregel den natürlichen Logarithmus ab.

Da $\bar{f}(x)=ln(x)$ ist $f(x)=e^x$. Setzte diese entsprechend (teilweise ja die Ableitung) in die Formel $\bar{f}'(x)=\frac{1}{f'(\bar{f}(x))}$ ein.

$\bar{f}'(x)=\frac{1}{f'(\bar{f}(x))}$

$\bar{f}'(x)=\frac{1}{e^{ln(x)}}=\frac{1}{x}$

4. Ein paar Ableitungen zum "warm" werden.

Berechne von den folgenden Funktionen jeweils die erste und zweite Ableitung in deinem Heft.

Beachte, dass bei $ln$-Funktionen meistens die Ketten-, Produkt- und Quotientenregel zum Ableiten gebraucht werden. Falls du diese nicht mehr kennst, kannst du jeweils in dem entsprechenden Tipp nachschauen.

a) $f(x)=ln(5x)$

b) $g(x)=3x^2\cdot ln(x)$

c) $h(x)=\frac{ln(x)}{x}$

$f(x)=v(u(x))$, dann $f'(x)=v'(u(x))\cdot u'(x)$

$f(x)=v(x)\cdot u(x)$, dann $f'(x)=v'(x)\cdot u(x)+v(x)\cdot u'(x)$

$f(x)=\frac{v(x)}{u(x)}$, dann $f'(x)=\frac{v'(x)\cdot u(x)-v(x)\cdot u'(x)}{u(x)^2}$

1. Ableitung: (Kettenregel) $f'(x)=\frac{1}{5x}\cdot 5=\frac{5}{5x}=\frac{1}{x}$

2. Ableitung: $f''(x)=(\frac{1}{x})'=(x^{-1})'=-x^{-2}=-\frac{1}{x^2}$

1. Ableitung: (Produktregel) $g'(x)=6x\cdot ln(x)+3x^2\cdot \frac{1}{x}=6x\cdot ln(x)+\frac{3x^2}{x}=6x\cdot ln(x)+3x$

2. Ableitung: (Produktregel) $g''(x)=6\cdot ln(x)+6x\cdot\frac{1}{x}+3=6\cdot ln(x)+\frac{6x}{x}+3=6\cdot ln(x)+6+3=6\cdot ln(x)+9$

1. Ableitung: (Quotientenregel) $h'(x)=\frac{\frac{1}{x}\cdot x-ln(x)\cdot 1}{x^2}=\frac{\frac{x}{x}-ln(x)}{x^2}=\frac{1-ln(x)}{x^2}$

2. Ableitung: (Quotientenregel) $h''(x)=\frac{-\frac{1}{x}\cdot x^2-(1-ln(x))\cdot 2x}{x^4}=\frac{-\frac{x^2}{x}-2x+2x\cdot ln(x)}{x^4}=\frac{-x-2x+2x\cdot ln(x)}{x^4}=\frac{-3x+2x\cdot ln(x)}{x^4}=\frac{x(-3+2ln(x))}{x^4}=\frac{-3+2ln(x)}{x^3}$

5. Ableiten verschiedener $ln$-Funktionen

Leite die folgenden (orangenen) Funktionen in deinem Heft ab und ordne sie dann ihrer Ableitung zu. Löse die Aufgabe nicht durch Ausprobieren! Notiere die eventuelle Fragen oder Unklarheiten.

6. Die Stammfunktion des natürlichen Logarithmus

Die Stammfunktion des natürlichen Logarithmus ist definiert durch:

$\bar{F}(x)=\int ln(x) dx=x\cdot ln(x)-x+c$.

(Die Integration kann man mit Hilfe partieller Integration durchführen.)

Aufgabe: Weise nach, dass die obige Funktion $\bar{F}(x)$ die Stammfunktion von $\bar{f}(x)=ln(x)$ ist.

Leite $\bar{F}(x)=x\cdot ln(x)-x+c$ ab.

$\bar{F}'(x)=(x\cdot ln(x)-x+c)'= 1\cdot ln(x)+x\cdot \frac{1}{x}-1=ln(x)+1-1=ln(x)=\bar{f}(x)$

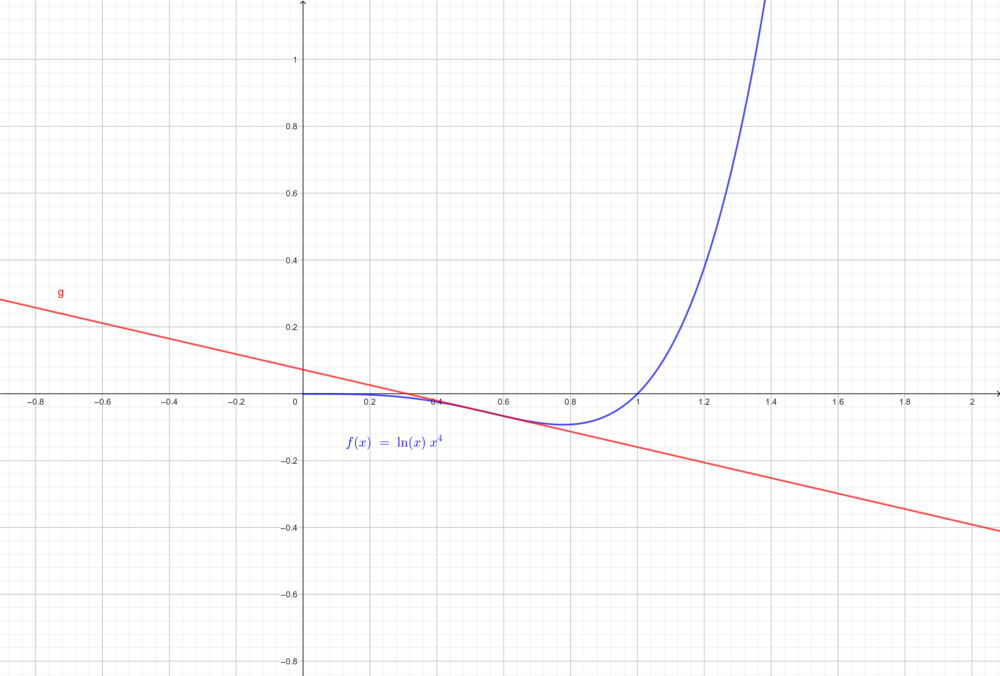
7. Kurvendiskussion ohne GTR

Gegeben ist die Funktion $f(x)=ln(x)\cdot x^4$.

a) Untersuche diese hinsichtlich des Definitionsbereiches, der Symmetrie, der Schnittpunkte mit den Koordinatenachsen, dem Unendlichkeitsverhalten der Extrempunkte und der Wendepunkte.

b) Die Wendetangente $g(x)$ begrenzt mit den Koordinatenachsen ein Flächenstück im 1. Quadranten. Berechne den Flächeninhalt dieses Stückes.

Die Wendetangente ist die Tangente, die den Funktionsgraphen am Wendepunkt berührt. Dementsprechend stimmt der dortige Ableitungswert mit der Steigung der Tangenten überein.

Das Flächenstück, welches eine Gerade mit den Koordinatenachsen einschließt, ist ein Dreieck.