Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Drei-Würfel-Problem: Unterschied zwischen den Versionen
Main>Florian Bogner K (Weiter...) |
Main>Florian Bogner |
||
| Zeile 5: | Zeile 5: | ||
*Zufallsexperiment auf Laplace-Experiment zurückführen (z.B. Kugeln durchnummerieren)--> | *Zufallsexperiment auf Laplace-Experiment zurückführen (z.B. Kugeln durchnummerieren)--> | ||
= Das „Drei-Würfel-Problem“ = | |||
Bild von drei Würfeln einfügen! | Bild von drei Würfeln einfügen! | ||
{{Kasten Mathematik|Das „Drei-Würfel-Problem“ stammt von ''Chevalier de Méré'' (1607 - 1684), einem französischen Edelmann im Zeitalter des Barocks. Er behauptete, dass die Augensummen 11 und 12 beim dreifachen Würfelwurf gleichwahrscheinlich | {{Kasten Mathematik|Das „Drei-Würfel-Problem“ stammt von ''Chevalier de Méré'' (1607 - 1684), einem französischen Edelmann im Zeitalter des Barocks. Er behauptete, dass die Augensummen 11 und 12 beim dreifachen Würfelwurf gleichwahrscheinlich sind. | ||
Für die Augensumme 11 gibt es sechs verschiedene Möglichkeiten: | Für die Augensumme 11 gibt es nämlich sechs verschiedene Möglichkeiten: | ||
<math>\left\{ 1,4,6 \right\}, \left\{ 1,5,5 \right\}, \left\{ 2,3,6 \right\}, \left\{ 2,4,5 \right\}, \left\{ 3,3,5 \right\}, \left\{ 3,4,4 \right\}</math> | <math>\left\{ 1,4,6 \right\}, \left\{ 1,5,5 \right\}, \left\{ 2,3,6 \right\}, \left\{ 2,4,5 \right\}, \left\{ 3,3,5 \right\}, \left\{ 3,4,4 \right\}</math> | ||
| Zeile 32: | Zeile 32: | ||
Wähle an der rechten Seite für die Augensumme 11 „Player A“ und für die Augensumme 12 „Player B“. Mit „Start the race“ geht es los! Du kannst auch automatisch viele Rennen durchlaufen lassen und die Gewinnerstatistik betrachten. | Wähle an der rechten Seite für die Augensumme 11 „Player A“ und für die Augensumme 12 „Player B“. Mit „Start the race“ geht es los! Du kannst auch automatisch viele Rennen durchlaufen lassen und die Gewinnerstatistik betrachten. | ||
{{Aufgaben-M|2| | {{Aufgaben-M|2|Berechne die Wahrscheinlichkeiten der Augensummen 11 und 12 beim zweifachen Würfelwurf! | ||
(Info: Bei dieser Aufgabe irrte sich übrigens ''Gottfried Wilhelm Freiherr von Leibniz'' (1646 - 1716), einer der letzten Universalgelehrten.)}} | |||
Tipp: Was fällt dir an den Würfeln im Spiel auf? Zeichne ein Baumdiagramm für die Augensummen 11 und 12 beim zweifachen Würfelwurf. | |||
Lösungshilfe: Mit Hilfe dieser [http://www.mathematik.uni-dortmund.de/didaktik/_personelles/papers/stoc_pro/Urne/JavaUrne.html Urnensimulation] kannst du | |||
{{Lösung versteckt|Die Würfel sind unterschiedlich gefärbt. Man könnte auch sagen: ''1. Wurf ist rot, 2. Wurf ist grün''. | |||
Damit wäre die Lösung nach ''de Méré'' der Art, dass es eine Möglichkeit für beide Augensummen gibt, nämlich <math>\left\{ 5,6 \right\}</math> beziehungsweise <math>\left\{ 6,6 \right\}</math>, falsch. | |||
Das Baumdiagramm zeigt zwei Wege, welche die Augensumme 11 ergeben. <math>\left\{ 5,6 \right\}, \left\{ 6,5 \right\}</math> <br!> [[Datei:Baum1.jpg]]}} | |||
{{Aufgaben-M|3|Löse nun Aufgabe 1, indem du die Wahrscheinlichkeiten für die Augensummen berechnest.}} | |||
Lösungshilfe: Mit Hilfe dieser [http://www.mathematik.uni-dortmund.de/didaktik/_personelles/papers/stoc_pro/Urne/JavaUrne.html Urnensimulation] kannst du einen dreifachen Würfelwurf simulieren. Dann kannst du erkennen wie viele Elemente der Ergebnisraum des dreifachen Würfelwurfs enthält. (→ Wie geht das? {{versteckt|6 Kugeln in der Urne; dreimaliges Ziehen mit zurücklegen und Beachtung der Reihenfolge.}}) | |||
==Übung== | ==Übung== | ||
Version vom 1. September 2009, 17:14 Uhr
Laplace-Experimente
Gleichwahrscheinlichkeit (z.B. mit Selbsdtversuch überprüfen)
- Ausblick auf Zufallsexperimente, die der Laplace-Annahme nicht genügen
- Zufallsexperiment auf Laplace-Experiment zurückführen (z.B. Kugeln durchnummerieren)-->
Das „Drei-Würfel-Problem“
Bild von drei Würfeln einfügen!
Sollte das Problem noch zu schwierig sein, vereinfache es zunächst auf den zweifachen Würfelwurf!
Auf folgender englischsprachigen Seite kannst du ein Spiel zum zweifachen Würfelwurf durchführen: Racing Game with two Dice (deutsch: Wettkampf mit zwei Würfeln)
Wähle an der rechten Seite für die Augensumme 11 „Player A“ und für die Augensumme 12 „Player B“. Mit „Start the race“ geht es los! Du kannst auch automatisch viele Rennen durchlaufen lassen und die Gewinnerstatistik betrachten.
Tipp: Was fällt dir an den Würfeln im Spiel auf? Zeichne ein Baumdiagramm für die Augensummen 11 und 12 beim zweifachen Würfelwurf.
Die Würfel sind unterschiedlich gefärbt. Man könnte auch sagen: 1. Wurf ist rot, 2. Wurf ist grün.
Damit wäre die Lösung nach de Méré der Art, dass es eine Möglichkeit für beide Augensummen gibt, nämlich beziehungsweise , falsch.
Das Baumdiagramm zeigt zwei Wege, welche die Augensumme 11 ergeben. <br!>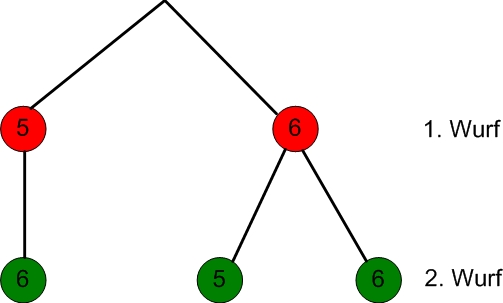
Lösungshilfe: Mit Hilfe dieser Urnensimulation kannst du einen dreifachen Würfelwurf simulieren. Dann kannst du erkennen wie viele Elemente der Ergebnisraum des dreifachen Würfelwurfs enthält. (→ Wie geht das? Vorlage:Versteckt)



