Grundlagen der Wahrscheinlichkeitsrechnung/Einführung in die Wahrscheinlichkeitsrechnung/Wahrscheinlichkeit: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 263: | Zeile 263: | ||
{{Vorlage:Grundlagen der Wahrscheinlichkeitsrechnung}} | {{Vorlage:Grundlagen der Wahrscheinlichkeitsrechnung}} | ||
{{SORTIERUNG:{{SUBPAGENAME}}}} | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie: | [[Kategorie:Mathematik]] | ||
[[Kategorie:Sekundarstufe 1]] | |||
[[Kategorie:Stochastik]] | |||
[[Kategorie:Wahrscheinlichkeitsrechnung]] | |||
[[Kategorie:Lernpfad]] | [[Kategorie:Lernpfad]] | ||
[[Kategorie: | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie:Mathematik-digital]] | [[Kategorie:Mathematik-digital]] | ||
[[Kategorie:ZUM2Edutags]] | [[Kategorie:ZUM2Edutags]] | ||
Version vom 8. September 2018, 12:43 Uhr
Kommen wir nun zum wohl wichtigsten Begriff der Wahrscheinlichkeitsrechnung: Die Wahrscheinlichkeit !
Was sind Wahrscheinlichkeiten?
Unter Wahrscheinlichkeit versteht man die Chance, dass bei einem Zufallsexperiment ein bestimmtes Ereignis auftritt.
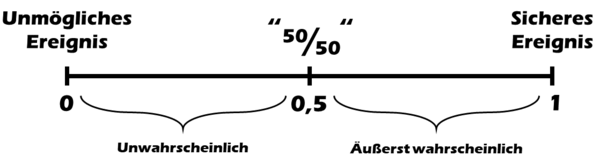
Wahrscheinlichkeiten werden Werte zwischen 0 und 1 zugeordnet. Dabei entspricht die 0, dass das Ereignis mit Sicherheit nicht eintreten kann (unmögliches Ereignis). Bei der Wahrscheinlichkeit 1 trifft das Ereignis mit Sicherheit ein (sicheres Ereignis).
Schreibweise:
P(A) = 0,5 (sprich: Die Wahrscheinlichkeit von Ereignis A ist 0,5)
Zur Veranschaulichung einer Wahrscheinlichkeit kann man sich folgenden Maßstab vorstellen:
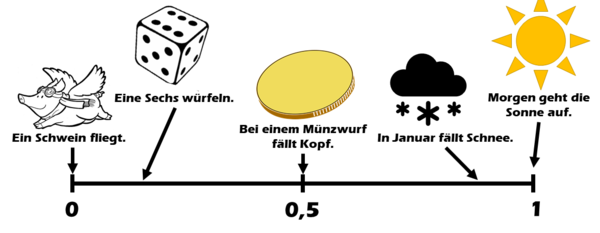
Hier sind einige Beispiele von Ereignissen, die auf dem Maßstab eingeordnet sind:
Multipliziert man die ausgerechnete Wahrscheinlichkeit mit dem Faktor 100, so erhält man das Prozentmaß der Wahrscheinlichkeit:
Eine Wahrscheinlichkeit von 0,12 entspricht also eine Wahrscheinlichkeit von 0,12*100 = 12%.
Wie bestimmt man Wahrscheinlichkeiten?
Um Wahrscheinlichkeiten bei einem Zufallsexperiment zu bestimmen, gibt es verschiedene Strategien. Zwei werdet ihr in diesem Lernpfad kennenlernen.
Die erste Strategie habt ihr im Einstiegsbeispiel schon mithilfe der Applets kennengerlernt: Wenn die Wahrscheinlichkeiten für bestimmte Ereignisse nicht bekannt oder gegeben sind, wiederholt ihr das Zufallsexperiment häufig, um die Wahrscheinlichkeit schätzen zu können.
Bei genügend großer Anzahl von Wiederholungen des Zufallsexperiments nähern sich die relativen Häufigkeiten der Ereignisse den theoretischen Wahrscheinlichkeiten dieser Ereignisse an. Dieser Zusammenhang wird mit dem Gesetz der großen Zahlen bezeichnet.
Eine Frage bleibt euch dabei sicherlich:
Wie oft muss man das Zufallsexperiment wiederholen, um die Wahrscheinlichkeit zu erhalten?
Dies kann man nicht eindeutig beantworten. Das Gesetz der großen Zahlen besagt nur, dass die realtiven Häufigkeiten bei ein größerer Anzahl von Wiederholungen näher an den theoretischen Wahrscheinlichkeiten liegen.
Oder anders gesagt: Je öfter wir das Zufallsexperiment wiederholen, desto mehr nähern sich die realtiven Häufigkeiten den theoretischen Wahrscheinlichkeiten an.
Das Gesetz der großen Zahlen sagt nichts darüber aus, wie die absoluten Verteilungen einer Zufallsversuchsreihe aussehen muss. Das heißt, dass wenn man relativ gesehen in einem Spiel sehr wenig 6en gewürfelt hat, nicht automatisch in den nächsten Runden viele 6en fallen müssen, um den Rückstand auszugleichen.
Ein Rückstand eines Ergebnisses wird also in zukünftigen Durchführungen eines Zufallsexperiments nicht ausgeglichen, dies ist leider ein weitverbreiteter Irrtum!
Die andere Strategie ist auf Laplace-Experimenten anwendbar. Was das sind erfahrt ihr auf der nächsten Seite !
Beispiel für das Abschätzen von Wahrscheinlichkeiten
Ein Achter-Legostein wird wiefolgt mit Zahlen von 1 bis 6 beschriftet, damit er als Würfel dienen kann:
Die Augenzahl 2 ist auf der Unterseite des Legosteins.
Da die Form und die Flächen des Lego-Würfels sehr unregelmäßig sind, kann man die Wahrscheinlichkeit der Augenzahlen am besten durch die häufige Durchführung des Zufallsexperiments bestimmen.
Nun wurde 2000-mal der Legowürfel geworfen und es kam folgendes Ergebnis raus:
| Augenzahl | Eins | Zwei | Drei | Vier | Fünf | Sechs |
|---|---|---|---|---|---|---|
| abs. Häufigkeit | 24 | 980 | 18 | 176 | 160 | 642 |
| rel. Häufigkeit | 0,012 | 0,49 | 0,009 | 0,088 | 0,08 | 0,321 |
Durch das Gesetz der großen Zahlen können wir nun annehmen, dass die Wahrscheinlicheiten in etwa mit den relativen Häufigkeiten übereinstimmen. Das heißt:
Die Augenzahl 1 fällt mit einer Wahrscheinlichkeit von 0,012, also etwa 1,2%.
Die Augenzahl 2 fällt mit einer Wahrscheinlichkeit von 0,49, also etwa 49%.
Die Augenzahl 3 fällt mit einer Wahrscheinlichkeit von 0,009, also etwa 0,9%.
Die Augenzahl 4 fällt mit einer Wahrscheinlichkeit von 0,088, also etwa 8,8%.
Die Augenzahl 5 fällt mit einer Wahrscheinlichkeit von 0,08, also etwa 8%.
Die Augenzahl 6 fällt mit einer Wahrscheinlichkeit von 0,321, also etwa 32,1%.
Aufgaben
Ihr führt folgende Zufallsexperimente 100-mal durch:
- a) Ihr werft einen normalen Würfel und betrachtet die Augenzahl als Ergebnis.
- Wie oft schätzt ihr, dass die Augenzahl 4 fällt? Begründe deine Antwort und tausche dich mit deinem Übungspartner aus!
- b) Ihr dreht folgendes Glücksrad und betrachtet die Farbe auf dem es stehen bleibt:
Lösung für a):
Man kann schätzen, dass die 4 etwa 17-mal vorkommt. (Der genaue Wert schwankt natürlich um die 17 herum)
Warum? : Ein Würfel hat 6 verschiedene Augenzahlen und alle sollten mit der gleichen Wahrscheinlichkeit fallen, da der Würfel regelmäßig ist und alle Flächen gleich groß sind. Bei 100 Versuchen sollte also jede Augenzahl ungefähr gleich viel fallen: , also ca. etwa 17-mal.
Lösung für b):
Man kann schätzen, dass die Frabe rot etwa 25-mal vorkommt.
Warum? : Das Glücksrad hat 8 verschiedene Sektoren, davon sind 2 rot. Jeder Sektor wird mit gleicher Wahrscheinlichkeit vorkommen, da sie gleich groß sind: , also sollte jeder Sektor etwa 12- bis 13-mal vorkommen. Da die Farbe Rot zwei Sektoren einnimmt, kann man schätzen, dass rot 2 * 12,5, also etwa 25-mal vorkommt.
Kontrolleure in der Bahn haben in der letzten Zeit 1235 Fahrgäste auf einen gültigen Fahrschein kontrolliert. Darunter waren 87 Schwarzfahrer.
- a) Wie wahrscheinlich ist, dass ein Kontrolleur einen Schwarzfahrer bei der nächsten Kontrolle erwischt?
Hier wurde das Zufallsexperiment, ob ein Passagier ein Schwarzfahrer ist, insgesamt 1235-mal durchgeführt und 87-mal kam das Ergebnis Schwarzfahrer dabei heraus. Durch das Gesetz der großen Zahlen können wir die relative Häufigkeit als theoretische Wahrscheinlichkeit annehmen. Daher gilt:
P("Der Kontrolleur erwischt einen Schwarzfahrer")=
Ein Kontrolleur erwischt einen Schwarzfahrer mit einer Wahrscheinlichkeit von ca. 7%.- b) Mit wie viel Verlust muss der Verkehrsbetrieb jährlich rechnen, wenn er monatlich 45.000 Fahrgäste befördert und ein Fahrschein 2,70€ kostet?
Der Verkehrsbetrieb transportiert jährlich 45.000*12 = 540.000 Fahrgäste.
Da mit einer Wahrscheinlichkeit von 7% ein Passagier Schwarzfahrer ist, gibt es im Jahr 540.000*0,07 = 37.800 Schwarzfahrer.
Das macht einen Verlust von 37.800*2,70€ = 102.060€.
Man kann mithilfe von statistischen Erhebungen und dem Gesetz der großen Zahlen Prognosen für zukünftige Gewinne/Verluste berechnen!
Gegeben ist folgendes Zufallsexperiment:
Ein zwölfseitiger Würfel wird geworfen und es wird die geworfene Augenzahl betrachtet. Man möchte wissen, wie wahrscheinlich es ist, dass eine Zahl fällt, die durch 4 teilbar ist.
Ordne den Fachbegriffen den konkreten Angaben zu diesem Würfelexperiment zu.
| Ergebnismenge | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} |
| Ereignis | "Es fällt eine Zahl, die durch 4 teilbar ist" |
| Ereignismenge | {4, 8, 12} |
| Wahrscheinlichkeit | P(E) = 0,25 |
| Wahrscheinlichkeit in Prozent | 25% |
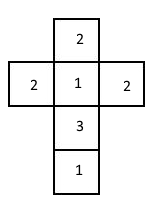
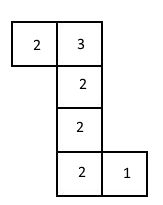
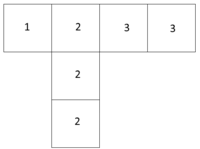
Ihr seht hier Würfelnetze dreier verschiedener Würfel:
Johann hat mit einem der Würfel 125 Würfe gemacht und die Augenzahl bei jedem Wurf notiert. Hier ist seine Tabelle mit den Häufigkeiten:
| Augenzahl | Eins | Zwei | Drei |
|---|---|---|---|
| Häufigkeit | 36 | 69 | 20 |
Mit welchem Würfel hat Johann wohl geworfen? Begründe deine Antwort!
Johann hat am wahrscheinlichsten mit dem Würfel 1) geworfen.
Anhand den Häufigkeiten, kann man die relativen Häufigkeiten und damit auch gleich die theoretischen Wahrscheinlichkeiten der Augenzahlen des Würfels bestimmen:
Für die Augenzahl eins gilt: 36/125 = 0,288 => Das entspricht einer Wahrscheinlichkeit von ca. 28,8%
Für die Augenzahl zwei gilt: 69/125 = 0,552 => Das entspricht einer Wahrscheinlichkeit von ca. 55,2%
Für die Augenzahl drei gilt: 20/125 = 0,16 => Das entspricht einer Wahrscheinlichkeit von ca. 16%
Betrachtet man nun die Würfelnetze, kann man feststellen, dass bei dem Würfelnetz 1) und 3) die Augenzahl zwei genau die Hälfte der Seiten des Würfels einnimmt => Die zwei sollte also etwa mit 50% Wahrscheinlichkeit beim Werfen fallen (das ist hier mit 55,2% der Fall)
Anhand den ausgerechneten Wahrscheinlichkeiten kann man auch feststellen, dass die Augenzahl eins öfter gefallen ist, als die Augenzahl drei => Die eins sollte also mehr Seiten des Würfels beanspruchen, als die drei.
Dies ist beim Würfelnetz 1) der Fall!
Gut zu wissen: An diesem Beispiel kann man gut erkennen, dass die die relativen Häufigkeiten bei geringer Anzahl an Versuchsdurchführungen von der theoretischen Wahrscheinlichkeit (mitunter auch stark) abweichen können. Daher können wir nicht mit Sicherheit sagen, dass das Würfelnetz 2 benutzt wurde, sondern es nur mit hoher Wahrscheinlichkeit annehmen.
Im Jahr 2017 gibt es 136,3 Mio. zahlende Nutzer von Musik-Streamingdiensten
Folgende Nutzerzahlen wurden dabei ermittelt:
| Spotify | Apple Music | Amazon Music | Andere |
|---|---|---|---|
| 54,52 Mio | 25,897 Mio | 16,356 Mio | 39,527 Mio |
Auf der Straße wird zufällig ein zahlender Nutzer von einem Streamindienst getroffen. Wie wahrscheinlich ist es...
- a) dass er Kunde von Amazon Music ist?
- b) dass er nicht Kunde von Apple Music ist?
- c) dass er Kunde von Spotify oder einem anderen (Andere) Dienst ist?
Ihr könnt euch unter diesem Link, die Statistik ansehen, auf dem diese Aufgabe beruht: https://de.statista.com/infografik/10431/weltweite-marktanteile-musik-streaming-anbieter/
Lösung für a):
Wir können aufgrund der hohen Wiederholungsanzahl des Zufallsexperiments (136,6 Mio-mal), die relative Häufigkeit als theoretische Wahrscheinlichkeit annehmen.
Daher gilt:
P("Kunde von Amazon Music") =
Mit einer Wahrscheinlichkeit von ca. 12% ist der Nutzer ein Kunde von Amazon Music.
Lösung für b):
Hier wird gefragt, wie wahrscheinlich es ist, dass der Nutzer NICHT Kunde von Apple Music ist.
Hierfür berechnet man die Wahrscheinlichkeit, dass er Kunde von einem der anderen Dienste ist. Dazu zählt man alle Kundenzahlen von allen Streamindiensten zusammen, die nicht Apple Music sind:
54,52 Mio. (Spotify) + 16,356 Mio. (Amazon Music) + 39,527 Mio. (Andere) = 110,403 Mio.
Also ergibt sich für die Wahrscheinlichkeit, dass man bei einem der andere Dienste ist:
P("nicht bei Apple Music") =
Mit einer Wahrscheinlichkeit von 80,82% ist der Nutzer NICHT bei Apple Music.
Lösung für c):
Hierfür zählt man die Kundenzahlen von Spotify und Andere zusammen:
54,52 Mio. (Spotify) + 39,527 Mio. (Andere) = 94,047 Mio.
Daher ergibt sich für die Wahrscheinlichkeit:
P("bei Spotify oder bei Andere") =
Mit einer Wahrscheinlichkeit von 68,85% ist der Nutzer bei Spotify oder einem der anderen Dienste.| Zurück zur letzten Seite | ............. | oder | ............. | Weiter zur nächsten Seite |
- Weißt du noch? Absolute und relative Häufigkeiten
- Einstiegsproblem: Die zufällige Shuffle-Funktion
- Simulation der Shuffle-Funktion
- Noch mehr Simulation zur Shuffle-Funktion
- Abschluss des Einstiegsproblems
- Einführung in die Wahrscheinlichkeitsrechnung