Grundlagen der Wahrscheinlichkeitsrechnung/Einführung in die Wahrscheinlichkeitsrechnung/Laplace-Experiment
Du hast schon eine Strategie zur Bestimmung von Wahrscheinlichkeiten durch das Gesetz der großen Zahlen kennengelernt. Nun lernst du noch eine weitere Strategie kennen, wie man Wahrscheinlichkeiten bei bestimmten Zufallsexperimenten bestimmen kann.
Zum Überlegen
| Datei:Idee-Icon.png | Wir hatten bei der Shuffle-Funktion festgestellt, das alle Lieder gleichwahrscheinlich abgespielt werden.
Überlege dir weitere Zufallsexperimente, bei dem alle Ausgänge gleichwahrscheinlich sind. Welche sind dir im Alltag schon begegnet? Tausche dich anschließend mit deinem Übungspartner aus. |
Definition: Laplace Experiment
| Datei:Definition-Icon.png | Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit besitzen. Alle Ausgänge des Experiments sind also gleichwahrscheinlich. |
Wie bestimmt man bei einem Laplace-Experiment nun Wahrscheinlichkeiten?
Dies geht ganz simpel mit dem folgenden Zusammenhang:
Um die Wahrscheinlichkeit eines Ereignisses zu bestimmen, teilt man einfach die Anzahl der günstigen Ergebnisse für das Ereignis durch die Anzahl aller möglichen Ergebnisse.
Es kommt auf die Betrachtung der Ergebnismenge an:
Ob Laplace-Experiment oder nicht, entscheidet die Ergebnismenge, die man betrachtet.
Betrachtet folgendes Zufallsexperiment:
Man zieht eine der Kugeln aus der Urne. Es gibt 1 grüne und 3 blaue Kugeln. Jede Kugel ist mit einer 1 oder 2 beschriftet.
Betrachtet man als Ergebnis die Zahlen auf den Kugeln, dann ergibt sich als Ergebnismenge {1, 2}. Es handelt sich um ein Laplace-Experiment, da jede Zahl zweimal gezogen werden kann und damit jedes Ergebnis gleichwahrscheinlich ist.
Betrachtet man als Ergebnis die Farbe, dann ergibt sich als Ergebnismenge {grün, blau} und es handelt sich nicht um ein Laplace-Experiment, da es wahrscheinlicher ist eine blaue als eine grüne Kugel zu ziehen.
Beispiel
Aufgaben zu Laplace-Experimenten
Aufgabe 1:
Bei welchem Zufallsexperimenten handelt es sich um Laplace-Experimente? (Werfen einer Münze) (! Ein Würfel mit der Beschriftung 1,2,3,4,1,2) (Ziehen einer Karte aus einem Kartenstapel von 52 Karten) (! Ziehen eines Loses aus einem Lostopf) (! Ziehen aus einer Urne mit 7 roten und 6 blauen Kugeln) (Ziehen aus einer Urne mit 12 unterschiedlichen Kugeln)
Aufgabe 2: Urne mit Kugeln
In einer Urne befinden sich 20 Kugeln, die mit den Zahlen von 1 bis 20 beschriftet sind.
Felix zieht eine Kugel. Mit welcher Wahrscheinlichkeit...
- a) zieht er die Kugel mit der Zahl 12?
- b) zieht er eine Zahl, die durch 3 teilbar ist?
- c) zieht er eine Zahl, die größer als 11 ist?
- d) zieht er eine Quadratzahl?
Schreibe für jede Teilaufgabe die passenden Ereignismengen auf.
<popup name="Lösung"> Es handelt sich um ein Laplace-Experiment, da jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird. Es gibt insgesamt 20 mögliche Ergebnisse bei der Ziehung
- a) Die Ereignismenge ist: A = {12}
- In der Ereignismenge ist also ein günstiges Ergebnis =>
- b) Die Ereignismenge ist: B = {3, 6, 9, 12, 15, 18}
- In der Ereignismenge sind also sechs günstige Ergebnisse =>
- c) Die Ereignismenge ist: C = {12, 13, 14, 15, 16, 17, 18, 19, 20}
- In der Ereignismenge sind also neun günstige Ergebnisse =>
- d) Die Ereignismenge ist: D = {1, 4, 9, 16}
- In der Ereignismenge sind also vier günstige Ergebnisse =>
</popup>
Aufgabe 3:
Drei Glücksräder
1.) 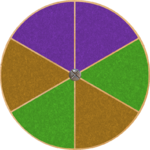 2.) Datei:Bogowheel.png 3.)
2.) Datei:Bogowheel.png 3.) 
- a) Welches der Glücksräder stellen keine Laplace-Experimente dar? Begründe deine Antwort!
- b) Wie wahrscheinlich ist es beim Glücksrad 1 die Farbe Orange zu bekommen?
- c) Wie wahrscheinlich ist es beim Glücksrad 3 das Ergebnis rot zu bekommen?
<popup name="Lösung">
- a) Glücksrad 2 ist kein Laplace-Experiment. Da die Farben unterschiedlich-große Sektoren einnehmen, sind die Farben beim Drehen nicht gleichwahrscheinlich. Es ist z.B. viel wahrscheinlicher auf Orange als auf pink zu landen.
- b) Es gibt insgesamt 6 gleichgroße Sektoren. 2 davon sind Orange. Daher gilt:
- c) Es gibt insgesamt 8 Sektoren, 2 davon sind rot. Daher gilt:
</popup>
Aufgabe 4:
Ein Kartenspiel hat 32 Karten mit den vier Farben: Herz, Karo, Pik und Kreuz. In jeder Farbe gibt es jeweils die Karten 7, 8, 9, 10, Bube, Dame, König und As.
Wie hoch ist die Wahrscheinlichkeit für folgende Ereignisse:
- a) Es wird eine Karte der Farbe Karo gezogen?
- b) Es wird eine Dame gezogen?
- c) Es wird nicht eine schwarze 10 gezogen?
- d) Es wird keine Bildkarte gezogen?
<popup name="Lösung">
Lösung für a):
In dem Kartendeck gibt es insgesamt 32 Karten, wovon 8 Karten der Farbe Karo angehören. Daher folgt:
P("Karo-Karte wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 25% eine Karo-Karte gezogen.
Lösung für b):
Es gibt 4 Damen in einem Kartendeck, daher gilt:
P("Dame wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 12,5% eine Dame gezogen.
Lösung für c):
Es gibt zwei schwarze 10 in Deck (Pik und Kreuz), daher folgt:
P("schwarze 10 wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 6,25% eine schwarze 10 gezogen.
Lösung für d):
Hier soll KEINE Bildkarte gezogen werden, man muss also die Anzahl der Karten zählen, die keine Bildkarten sind. Die 7,8,9,10 sind keine Bildkarten und von jeder Karte gibt es durch die unterschiedlichen Farben 4 Stück. Es gibt also insgesamt 16 Karten im Deck, die nicht zu den Bildkarten zählen, daher folgt:
P("keine Bildkarte wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 50% keine Bildkarte gezogen. </popup>
Aufgabe 5:
Zu sehen ist eine Urne, die noch keine Kugeln enthält.
Befülle für jede Teilaufgabe eine Urne so (selber skizzieren), dass folgende Wahrscheinlichkeiten eintreten:
Die Grundmenge der Kugeln kann bei jeder Teilaufgabe frei gewählt werden.
- a) Die Wahrscheinlichkeit eine blaue Kugel zu ziehen ist P("blaue Kugel") = 0,25.
- b) Die Wahrscheinlichkeit eine rote Kugel zu ziehen ist P("rote Kugel") = 0,10.
- c) Die Wahrscheinlichkeit eine grüne Kugel zu ziehen ist P("grüne Kugel") = 0,15.
- d) Die Wahrscheinlichkeit eine gelbe Kugel zu ziehen ist P("gelbe Kugel") = 0,50.
- e) alle Wahrscheinlichkeiten aus a), b), c), d) sollen gleichzeitig eintreffen
<popup name="Lösung">
- a) z.B. bei 1 blaue Kugel und 3 Kugeln anderer Farbe.
- b) z.B. 1 rote Kugel und 9 Kugeln anderer Farbe.
- c) z.B. 3 grüne Kugel und 17 Kugeln anderer Farbe.
- d) z.B. 1 gelbe Kugel und 1 Kugel anderer Farbe.
- e) z.B. 10 gelbe Kugeln, 3 grüne Kugeln, 2 rote Kugeln und 5 blaue Kugeln.
</popup>