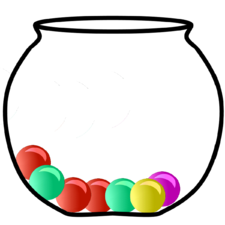Grundlagen der Wahrscheinlichkeitsrechnung/Einführung in die Wahrscheinlichkeitsrechnung/Laplace-Experiment: Unterschied zwischen den Versionen
K (87 Versionen importiert) |
(katfix) Markierung: 2017-Quelltext-Bearbeitung |
||
| (13 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Grundlagen der Wahrscheinlichkeitsrechnung}}|Lernschritte einblenden|Lernschritte ausblenden}} | |||
Du hast schon eine Strategie zur Bestimmung von Wahrscheinlichkeiten durch das Gesetz der großen Zahlen kennengelernt. Nun lernst du noch eine weitere Strategie kennen, wie man Wahrscheinlichkeiten bei bestimmten Zufallsexperimenten bestimmen kann. | Du hast schon eine Strategie zur Bestimmung von Wahrscheinlichkeiten durch das Gesetz der großen Zahlen kennengelernt. Nun lernst du noch eine weitere Strategie kennen, wie man Wahrscheinlichkeiten bei bestimmten Zufallsexperimenten bestimmen kann. | ||
== Zum Überlegen == | == Zum Überlegen == | ||
{ | {{Box||Wir hatten bei der Shuffle-Funktion festgestellt, das alle Lieder gleichwahrscheinlich abgespielt werden. | ||
Überlege dir weitere Zufallsexperimente, bei dem alle Ausgänge gleichwahrscheinlich sind. Welche sind dir im Alltag schon begegnet? | Überlege dir weitere Zufallsexperimente, bei dem alle Ausgänge gleichwahrscheinlich sind. Welche sind dir im Alltag schon begegnet? | ||
Tausche dich anschließend mit deinem Übungspartner/ deiner Übungspartnerin aus. | Tausche dich anschließend mit deinem Übungspartner/ deiner Übungspartnerin aus. | ||
|} | |Unterrichtsidee }} | ||
= Was ist ein Laplace-Experiment? = | = Was ist ein Laplace-Experiment? = | ||
{ | {{Box||Ein '''Laplace-Experiment''' ist ein Zufallsexperiment, bei dem alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit besitzen. Alle Ausgänge des Experiments sind also ''gleichwahrscheinlich''. | ||
| Hervorhebung2}} | |||
|} | |||
Wie bestimmt man bei einem Laplace-Experiment nun Wahrscheinlichkeiten? | Wie bestimmt man bei einem Laplace-Experiment nun Wahrscheinlichkeiten? | ||
Dies geht ganz simpel mit dem folgenden Zusammenhang: | Dies geht ganz simpel mit dem folgenden Zusammenhang: | ||
<math>P(E) = \frac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}} = \frac{\#E}{\#\Omega} </math> | |||
Um die Wahrscheinlichkeit eines Ereignisses zu bestimmen, teilt man einfach die ''Anzahl der günstigen Ergebnisse für das Ereignis'' durch die ''Anzahl aller möglichen Ergebnisse''. | Um die Wahrscheinlichkeit eines Ereignisses zu bestimmen, teilt man einfach die ''Anzahl der günstigen Ergebnisse für das Ereignis'' durch die ''Anzahl aller möglichen Ergebnisse''. | ||
| Zeile 55: | Zeile 51: | ||
== Aufgaben zu Laplace-Experimenten == | == Aufgaben zu Laplace-Experimenten == | ||
{{Box|1. Gewinnregeln vergleichen| | |||
In einem Würfel-Spiel gibt es folgende Spielregeln: Du würfelst einmal mit einem normalen Spielwürfel und... | In einem Würfel-Spiel gibt es folgende Spielregeln: Du würfelst einmal mit einem normalen Spielwürfel und... | ||
:a) du gewinnst bei einer geraden Zahl | :a) du gewinnst bei einer geraden Zahl | ||
:b) du gewinnst bei einer ungeraden Zahl | :b) du gewinnst bei einer ungeraden Zahl | ||
| Zeile 63: | Zeile 58: | ||
:d) du gewinnst, wenn eine Zahl größer 5 fällt. | :d) du gewinnst, wenn eine Zahl größer 5 fällt. | ||
*Für welche Spielregel würdest du dich entscheiden, um zu gewinnen? | *Für welche Spielregel würdest du dich entscheiden, um zu gewinnen? Begründe deine Antwort! | ||
*Berechne die Wahrscheinlichkeit zu gewinnen bei allen Spielregeln. | *Berechne die Wahrscheinlichkeit zu gewinnen bei allen Spielregeln. | ||
{{Lösung versteckt|1= | |||
Am besten du entscheidest dich für die Regel c), da es am wahrscheinlichsten ist eine Zahl kleiner 4 zu würfeln. | Am besten du entscheidest dich für die Regel c), da es am wahrscheinlichsten ist eine Zahl kleiner 4 zu würfeln. | ||
Es gibt nämlich 6 mögliche Ergebnisse bei einem Würfelwurf <math>\Omega =</math>{1, 2, 3, 4, 5, 6} und das Ereignis: C:"Es fällt eine Zahl kleiner 4" hat folgende Ereignismenge C={1, 2, 3, 4}, also 4 günstige Ergebnisse. Daher gilt für die Wahrscheinlichkeit von dem Ereignis C nach Laplace: | Es gibt nämlich 6 mögliche Ergebnisse bei einem Würfelwurf <math>\Omega =</math>{1, 2, 3, 4, 5, 6} und das Ereignis: C:"Es fällt eine Zahl kleiner 4" hat folgende Ereignismenge C={1, 2, 3, 4}, also 4 günstige Ergebnisse. Daher gilt für die Wahrscheinlichkeit von dem Ereignis C nach Laplace: | ||
| Zeile 83: | Zeile 76: | ||
:d) D: "Es fällt eine Zahl größer 4", die Ereignismenge lautet D={6} | :d) D: "Es fällt eine Zahl größer 4", die Ereignismenge lautet D={6} | ||
:P(D) = <math>\frac{1}{6} = 0,167</math>. | :P(D) = <math>\frac{1}{6} = 0,167</math>. | ||
}} | |||
|Üben}} | |||
{{Box|2. Welcher Würfel ist besser zum Gewinnen?| | |||
Du gewinnst, wenn du die Augenzahl 6 würfelst. Für welchen Würfel entscheidest du dich? | Du gewinnst, wenn du die Augenzahl 6 würfelst. Für welchen Würfel entscheidest du dich? | ||
| Zeile 91: | Zeile 85: | ||
Begründe deine Antwort, berechne dazu die Gewinnwahrscheilichkeiten für beide Würfel. | Begründe deine Antwort, berechne dazu die Gewinnwahrscheilichkeiten für beide Würfel. | ||
{{Lösung versteckt|1= | |||
Du entscheidest dich am besten für den Würfel 1). Denn der Würfel hat sechs mögliche Ergebnisse: <math>\Omega=</math>{1, 2, 3, 4, 5, 6} und es ist einmal die Augenzahl 6 dabei. Daher gilt für die Wahrscheinlichkeit eine 6 zu würfeln: | Du entscheidest dich am besten für den Würfel 1). Denn der Würfel hat sechs mögliche Ergebnisse: <math>\Omega=</math>{1, 2, 3, 4, 5, 6} und es ist einmal die Augenzahl 6 dabei. Daher gilt für die Wahrscheinlichkeit eine 6 zu würfeln: | ||
| Zeile 104: | Zeile 96: | ||
Es ist also wahrscheinlicher mit dem Sechsseiter eine 6 zu würfeln, als mit dem Achtseiter. | Es ist also wahrscheinlicher mit dem Sechsseiter eine 6 zu würfeln, als mit dem Achtseiter. | ||
}} | |||
|Üben}} | |||
{{Box|3. Welcher Würfel?| | |||
Zwei Würfel stehen für dich zur Auswahl: | Zwei Würfel stehen für dich zur Auswahl: | ||
| Zeile 114: | Zeile 107: | ||
:a) Du gewinnst, wenn du eine ungerade Zahl würfelst. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort! | :a) Du gewinnst, wenn du eine ungerade Zahl würfelst. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort! | ||
:b) Du gewinnst, wenn du eine Zahl würfelst, die durch 4 teilbar ist. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort! | :b) Du gewinnst, wenn du eine Zahl würfelst, die durch 4 teilbar ist. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort! | ||
{{Lösung versteckt|1= | |||
'''a)''': Der Sechsseiter hat mit den Augenzahlen 2, 4 und 6 drei gerade Zahlen. Daher gilt für die Wahrscheinlichkeit eine gerade Zahl zu würfeln: | '''a)''': Der Sechsseiter hat mit den Augenzahlen 2, 4 und 6 drei gerade Zahlen. Daher gilt für die Wahrscheinlichkeit eine gerade Zahl zu würfeln: | ||
| Zeile 138: | Zeile 128: | ||
Es ist wahrscheinlicher zu gewinnen, wenn man sich für den Zwölfseiter entscheidet. | Es ist wahrscheinlicher zu gewinnen, wenn man sich für den Zwölfseiter entscheidet. | ||
}} | |||
|Üben}} | |||
{{Box|4. Aus Urnen ziehen| | |||
Folgende Urnen sind gegeben: | Folgende Urnen sind gegeben: | ||
| Zeile 161: | Zeile 151: | ||
*Wenn du eine rote Kugel ziehen müsstest, um zu gewinnen, für welche Urne würdest du dich entscheiden? Begründe deine Antwort. | *Wenn du eine rote Kugel ziehen müsstest, um zu gewinnen, für welche Urne würdest du dich entscheiden? Begründe deine Antwort. | ||
Berechne die Wahrscheinlichkeit eine rote Kugel zu ziehen in beiden Urnen. | Berechne die Wahrscheinlichkeit eine rote Kugel zu ziehen in beiden Urnen. | ||
{{Lösung versteckt|1= | |||
'''Lösung für a)''': Du solltest dich für die Urne 2 entscheiden. Beide Urnen haben insgesamt 11 Kugeln im Gefäß, Urne 1 hat dabei vier rote Kugeln und die Urne 2 hat fünf rote Kugeln. Es ist also wahrscheinlicher eine rote Kugel aus der Urne 2 zu ziehen. | '''Lösung für a)''': Du solltest dich für die Urne 2 entscheiden. Beide Urnen haben insgesamt 11 Kugeln im Gefäß, Urne 1 hat dabei vier rote Kugeln und die Urne 2 hat fünf rote Kugeln. Es ist also wahrscheinlicher eine rote Kugel aus der Urne 2 zu ziehen. | ||
| Zeile 188: | Zeile 176: | ||
Da es wahrscheinlicher ist aus der Urne 1 eine rote Kugel zu ziehen, sollte man sich für die erste Urne entscheiden | Da es wahrscheinlicher ist aus der Urne 1 eine rote Kugel zu ziehen, sollte man sich für die erste Urne entscheiden | ||
}} | |||
|Üben}} | |||
{{Box|5. Urne mit Kugeln| | |||
In einer Urne befinden sich 20 Kugeln, die mit den Zahlen von 1 bis 20 beschriftet sind. | In einer Urne befinden sich 20 Kugeln, die mit den Zahlen von 1 bis 20 beschriftet sind. | ||
| Zeile 204: | Zeile 193: | ||
Schreibe für jede Teilaufgabe die passenden Ereignismengen auf. | Schreibe für jede Teilaufgabe die passenden Ereignismengen auf. | ||
{{Lösung versteckt|1= | |||
Es handelt sich um ein Laplace-Experiment, da jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird. Es gibt insgesamt 20 mögliche Ergebnisse bei der Ziehung | Es handelt sich um ein Laplace-Experiment, da jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird. Es gibt insgesamt 20 mögliche Ergebnisse bei der Ziehung | ||
| Zeile 223: | Zeile 211: | ||
:In der Ereignismenge sind also vier günstige Ergebnisse => <math>\frac{4}{20} = 0,2</math> | :In der Ereignismenge sind also vier günstige Ergebnisse => <math>\frac{4}{20} = 0,2</math> | ||
}} | |||
|Üben}} | |||
{{Box|6. Vergleich zweier Glücksräder| | |||
Du siehst hier zwei Glücksräder | Du siehst hier zwei Glücksräder | ||
| Zeile 231: | Zeile 220: | ||
:a) Du gewinnst, wenn das Glücksrad auf der Farbe Grün landet. | :a) Du gewinnst, wenn das Glücksrad auf der Farbe Grün landet. | ||
:Bei welchem ist die Gewinnchance höher? Begründe deine Antwort! | :Bei welchem ist die Gewinnchance höher? Begründe deine Antwort! | ||
:b) Wie wahrscheinlich ist es beim Glücksrad 1 einen Sektor zu bekommen, der neben einem grünen Sektor liegt? | :b) Wie wahrscheinlich ist es beim Glücksrad 1 einen Sektor zu bekommen, der neben einem grünen Sektor liegt? | ||
:c) Wieviele rote Sektoren müsste Glücksrad 2 haben, damit die Wahrscheinlichkeit für einen roten Sektor bei 75% liegt? | :c) Wieviele rote Sektoren müsste Glücksrad 2 haben, damit die Wahrscheinlichkeit für einen roten Sektor bei 75% liegt? | ||
{{Lösung versteckt|1= | |||
:a) Es ist besser sich für das 1. Glücksrad zu entscheiden, da es dort wahrscheinlicher ist auf grün zu landen. | :a) Es ist besser sich für das 1. Glücksrad zu entscheiden, da es dort wahrscheinlicher ist auf grün zu landen. | ||
Denn es gilt für das 1. Glücksrad: Es gibt insgesamt 6 gleichgroße Sektoren und 2 davon sind grün. Daher gilt für die Gewinnwahrscheinlichkeit: | Denn es gilt für das 1. Glücksrad: Es gibt insgesamt 6 gleichgroße Sektoren und 2 davon sind grün. Daher gilt für die Gewinnwahrscheinlichkeit: | ||
| Zeile 258: | Zeile 242: | ||
Es müssten also 6 Sektoren rot sein, damit bei dem Glücksrad 2 eine 75%-Wahrscheinlichkeit für einen roten Sektor ist. | Es müssten also 6 Sektoren rot sein, damit bei dem Glücksrad 2 eine 75%-Wahrscheinlichkeit für einen roten Sektor ist. | ||
}} | |||
|Üben}} | |||
{{Box|7. Gewinnregeln beim Glücksrad| | |||
Du siehst folgendes Glücksrad | Du siehst folgendes Glücksrad | ||
| Zeile 273: | Zeile 258: | ||
*Für welche Regel entscheidest du dich, um zu gewinnen? Begründe deine Antwort. | *Für welche Regel entscheidest du dich, um zu gewinnen? Begründe deine Antwort. | ||
{{Lösung versteckt|1= | |||
Um zu entscheiden, welche Gewinnregel die größte Chance hat zu gewinnen, sollte man die Wahrscheinlichkeiten zu den einzelnen Ereignissen der Regeln bestimmen: | Um zu entscheiden, welche Gewinnregel die größte Chance hat zu gewinnen, sollte man die Wahrscheinlichkeiten zu den einzelnen Ereignissen der Regeln bestimmen: | ||
| Zeile 287: | Zeile 270: | ||
Man sollte sich für die Regel c) entscheiden, da die Wahrscheinlichkeit zu gewinnen dort am größten ist. | Man sollte sich für die Regel c) entscheiden, da die Wahrscheinlichkeit zu gewinnen dort am größten ist. | ||
}} | |||
|Üben}} | |||
{{Box|8. Urne oder Würfel?| | |||
Du hast zwei Möglichkeiten dich für ein Gewinnspiel zu entscheiden: | Du hast zwei Möglichkeiten dich für ein Gewinnspiel zu entscheiden: | ||
| Zeile 303: | Zeile 286: | ||
Für welches Gewinnspiel entscheidest du dich? | Für welches Gewinnspiel entscheidest du dich? | ||
Berechne zur Begründung deiner Etscheidung die Gewinnwahrscheinlichkeiten der Spiele aus. | Berechne zur Begründung deiner Etscheidung die Gewinnwahrscheinlichkeiten der Spiele aus. | ||
{{Lösung versteckt|1= | |||
Man sollte sich für das Urne in dem Gewinnspiel entscheiden, da es dort wahrscheinlicher zu gewinnen. | Man sollte sich für das Urne in dem Gewinnspiel entscheiden, da es dort wahrscheinlicher zu gewinnen. | ||
| Zeile 313: | Zeile 296: | ||
P("Würfel") = <math>\frac{2}{6}</math> = 0,33 | P("Würfel") = <math>\frac{2}{6}</math> = 0,33 | ||
}} | |||
|Üben}} | |||
{{Box|9. Spielkarten ziehen| | |||
Ein Kartenspiel hat 32 Karten mit den vier Farben: Herz, Karo, Pik und Kreuz. | Ein Kartenspiel hat 32 Karten mit den vier Farben: Herz, Karo, Pik und Kreuz. | ||
In jeder Farbe gibt es jeweils die Karten 7, 8, 9, 10, Bube, Dame, König und Ass. | In jeder Farbe gibt es jeweils die Karten 7, 8, 9, 10, Bube, Dame, König und Ass. | ||
| Zeile 328: | Zeile 312: | ||
:d) Es wird keine Bildkarte gezogen? | :d) Es wird keine Bildkarte gezogen? | ||
{{Lösung versteckt|1= | |||
'''Lösung für a):''' | '''Lösung für a):''' | ||
| Zeile 362: | Zeile 344: | ||
Es wird also mit einer Wahrscheinlichkeit von 50% keine Bildkarte gezogen. | Es wird also mit einer Wahrscheinlichkeit von 50% keine Bildkarte gezogen. | ||
}} | |||
|Üben}} | |||
= | {{Box|1=10. Urnen befüllen|2= | ||
Zu sehen ist eine Urne, die noch keine Kugeln enthält. | Zu sehen ist eine Urne, die noch keine Kugeln enthält. | ||
| Zeile 379: | Zeile 362: | ||
:e) alle Wahrscheinlichkeiten aus a), b), c), d) sollen gleichzeitig eintreffen | :e) alle Wahrscheinlichkeiten aus a), b), c), d) sollen gleichzeitig eintreffen | ||
{{Lösung versteckt| | |||
Es ist einfacher sich zunächst über eine geeignete Menge an Kugeln in der Urne Gedanken zu machen. | Es ist einfacher sich zunächst über eine geeignete Menge an Kugeln in der Urne Gedanken zu machen. | ||
| Zeile 394: | Zeile 377: | ||
Jetzt müsst ihr nur überlegen, wie ihr die Kugeln einfärben müsst. | Jetzt müsst ihr nur überlegen, wie ihr die Kugeln einfärben müsst. | ||
|Hilfestellung|Verbergen}} | |||
{{Lösung versteckt| | |||
:a) z.B. bei 1 blaue Kugel und 3 Kugeln anderer Farbe. | :a) z.B. bei 1 blaue Kugel und 3 Kugeln anderer Farbe. | ||
| Zeile 406: | Zeile 389: | ||
:e) z.B. 10 gelbe Kugeln, 3 grüne Kugeln, 2 rote Kugeln und 5 blaue Kugeln. | :e) z.B. 10 gelbe Kugeln, 3 grüne Kugeln, 2 rote Kugeln und 5 blaue Kugeln. | ||
}} | |||
|3=Üben}} | |||
|} | |||
{{Fortsetzung|weiter=Zum Abschlusstest|weiterlink=../../Abschlusstest}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie: | [[Kategorie:Grundlagen der Wahrscheinlichkeitsrechnung]] | ||
Version vom 15. Mai 2020, 08:46 Uhr
Du hast schon eine Strategie zur Bestimmung von Wahrscheinlichkeiten durch das Gesetz der großen Zahlen kennengelernt. Nun lernst du noch eine weitere Strategie kennen, wie man Wahrscheinlichkeiten bei bestimmten Zufallsexperimenten bestimmen kann.
Zum Überlegen
Wir hatten bei der Shuffle-Funktion festgestellt, das alle Lieder gleichwahrscheinlich abgespielt werden. Überlege dir weitere Zufallsexperimente, bei dem alle Ausgänge gleichwahrscheinlich sind. Welche sind dir im Alltag schon begegnet?
Tausche dich anschließend mit deinem Übungspartner/ deiner Übungspartnerin aus.
Was ist ein Laplace-Experiment?
Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle möglichen Ergebnisse die gleiche Wahrscheinlichkeit besitzen. Alle Ausgänge des Experiments sind also gleichwahrscheinlich.
Wie bestimmt man bei einem Laplace-Experiment nun Wahrscheinlichkeiten?
Dies geht ganz simpel mit dem folgenden Zusammenhang:
Um die Wahrscheinlichkeit eines Ereignisses zu bestimmen, teilt man einfach die Anzahl der günstigen Ergebnisse für das Ereignis durch die Anzahl aller möglichen Ergebnisse.
Beispiel: Das Urnen-Experiment
Betrachtet folgendes Zufallsexperiment:
Man zieht eine der Kugeln aus der Urne. Da jede Kugel gleich groß ist, zieht man jede Kugel mit der gleichen Wahrscheinlichkeit. Es handelt sich also um ein Laplace-Experiment.
Wie wahrscheinlich ist es die Farbe grün zu ziehen?
- Betrachtet man die gezogene Farbe als Ergebnis, dann haben wir 1-mal die Farbe grün und 3-mal die Farbe blau in der Urne.
- Da es insgesamt 4 Kugeln gibt, folgt für die Wahrscheinlichkeit für die Farbe grün:
- P(grün) = , da eine der 4 Kugeln die gewünschte Farbe hat.
- Für blau gilt dementsprechend:
- P(blau) = , da 3 der 4 Kugeln die gewünschte Farbe haben.
Wie wahrscheinlich ist es die Zahl Zwei zu ziehen?
- Betrachtet man die gezogene Zahl als Ergebnis, dann haben wir 2-mal die Zahl Eins und 2-mal die Zahl Zwei in der Urne.
- Da es insgesamt 4 Kugeln gibt, folgt für die Wahrscheinlichkeit der Zahl Zwei:
- P(Zwei) = , da 2 der 4 Kugeln die gewünschte Zahl Zwei beschriftet haben.
Aufgaben zu Laplace-Experimenten
In einem Würfel-Spiel gibt es folgende Spielregeln: Du würfelst einmal mit einem normalen Spielwürfel und...
- a) du gewinnst bei einer geraden Zahl
- b) du gewinnst bei einer ungeraden Zahl
- c) du gewinnst, wenn eine Zahl kleiner 5 fällt
- d) du gewinnst, wenn eine Zahl größer 5 fällt.
- Für welche Spielregel würdest du dich entscheiden, um zu gewinnen? Begründe deine Antwort!
- Berechne die Wahrscheinlichkeit zu gewinnen bei allen Spielregeln.
Am besten du entscheidest dich für die Regel c), da es am wahrscheinlichsten ist eine Zahl kleiner 4 zu würfeln. Es gibt nämlich 6 mögliche Ergebnisse bei einem Würfelwurf {1, 2, 3, 4, 5, 6} und das Ereignis: C:"Es fällt eine Zahl kleiner 4" hat folgende Ereignismenge C={1, 2, 3, 4}, also 4 günstige Ergebnisse. Daher gilt für die Wahrscheinlichkeit von dem Ereignis C nach Laplace:
- P(C) = .
Für die anderen Gewinnregeln gelten folgende Wahrscheinlichkeiten:
- a) A: "Es fällt eine gerade Zahl", die Ereignismenge lautet A={2, 4, 6}
- P(A) = .
- b) B: "Es fällt eine ungerade Zahl", die Ereignismenge lautet B={1, 3, 5}
- P(B) = .
- d) D: "Es fällt eine Zahl größer 4", die Ereignismenge lautet D={6}
- P(D) = .
Du gewinnst, wenn du die Augenzahl 6 würfelst. Für welchen Würfel entscheidest du dich?
Begründe deine Antwort, berechne dazu die Gewinnwahrscheilichkeiten für beide Würfel.
Du entscheidest dich am besten für den Würfel 1). Denn der Würfel hat sechs mögliche Ergebnisse: {1, 2, 3, 4, 5, 6} und es ist einmal die Augenzahl 6 dabei. Daher gilt für die Wahrscheinlichkeit eine 6 zu würfeln:
P(A) = = 0,167
Für den Würfel unter 2) gilt: Die Ergebnismenge lautet: {1, 2, 3, 4, 5, 6, 7, 8}, wobei einmal die Augenzahl 6 vorkommt. Daher gilt für den Würfel 2) eine 6 zu würfeln:
P(B) = = 0,125
Es ist also wahrscheinlicher mit dem Sechsseiter eine 6 zu würfeln, als mit dem Achtseiter.
Zwei Würfel stehen für dich zur Auswahl:
- a) Du gewinnst, wenn du eine ungerade Zahl würfelst. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort!
- b) Du gewinnst, wenn du eine Zahl würfelst, die durch 4 teilbar ist. Für welchen Würfel würdest du dich entscheiden? Begründe deine Antwort!
a): Der Sechsseiter hat mit den Augenzahlen 2, 4 und 6 drei gerade Zahlen. Daher gilt für die Wahrscheinlichkeit eine gerade Zahl zu würfeln:
P("gerade Zahl bei Sechsseiter") = = 0,5
Der Zwölfseiter hat mit den Augenzahlen 2, 4, 6, 8, 10 und 12 sechs gerade Zahlen. Daher gilt für die Wahrscheinlichkeit eine gerade Zahl zu würfeln:
P("gerade Zahl bei Zwölfseiter") = = 0,5
Es ist also egal für welchen Würfel man sich entscheidet, da beide die gleiche Wahrscheinlichkeit zum Gewinnen haben.
b): Bei dem Sechsseiter ist nur die Augenzahl 4 durch vier teilbar. Daher gilt für die Wahrscheinlichkeit:
P("durch 4 teilbar bei Sechsseiter") = = 0,167
Bei dem Zwölfseiter sind die Augenzahlen 4, 8, und 12 durch vier teilbar. Daher gilt für die Wahrscheinlichkeit:
P("durch 4 teilbar bei Zwölfseiter") = = 0,25
Es ist wahrscheinlicher zu gewinnen, wenn man sich für den Zwölfseiter entscheidet.
Folgende Urnen sind gegeben:
- Wenn du eine rote Kugel ziehen müsstest, um zu gewinnen, für welche Urne würdest du dich entscheiden? Begründe deine Antwort.
Berechne die Wahrscheinlichkeit eine rote Kugel zu ziehen in beiden Urnen.
- Wenn du eine rote Kugel ziehen müsstest, um zu gewinnen, für welche Urne würdest du dich entscheiden? Begründe deine Antwort.
Berechne die Wahrscheinlichkeit eine rote Kugel zu ziehen in beiden Urnen.
- Wenn du eine rote Kugel ziehen müsstest, um zu gewinnen, für welche Urne würdest du dich entscheiden? Begründe deine Antwort.
Berechne die Wahrscheinlichkeit eine rote Kugel zu ziehen in beiden Urnen.
Lösung für a): Du solltest dich für die Urne 2 entscheiden. Beide Urnen haben insgesamt 11 Kugeln im Gefäß, Urne 1 hat dabei vier rote Kugeln und die Urne 2 hat fünf rote Kugeln. Es ist also wahrscheinlicher eine rote Kugel aus der Urne 2 zu ziehen.
Es gilt:
P("rote Kugel aus Urne 1") = = 0,36
P("rote Kugel aus Urne 2") = = 0,45
Lösung für b): Du solltest dich für die Urne 2 entscheiden. Beide Urnen haben insgesamt jeweils drei rote Kugeln im Gefäß, jedoch hat Urne 1 insgesamt 8 Kugeln im Gefäß und die Urne 2 insgesamt 7 Kugel. Es ist also wahrscheinlicher eine rote Kugel aus der Urne 2 zu ziehen, da die Chance größer ist aus einer kleineren Grundmenge eine der drei roten Kugeln zu ziehen.
Es gilt:
P("rote Kugel aus Urne 1") = = 0,375
P("rote Kugel aus Urne 2") = = 0,428
Lösung für c): Hier sind jeweils die Anzahl der roten Kugeln pro Urne, als auch die Anzahl aller Kugeln in den Urnen verschieden. Ein Vergleich der Gewinnchance wird mit einer Berechnung der Wahrscheinlichkeiten leicht zu bestimmen sein:
P("rote Kugel aus Urne 1") = = 0,385
P("rote Kugel aus Urne 2") = = 0,333
Da es wahrscheinlicher ist aus der Urne 1 eine rote Kugel zu ziehen, sollte man sich für die erste Urne entscheiden
In einer Urne befinden sich 20 Kugeln, die mit den Zahlen von 1 bis 20 beschriftet sind.
Felix zieht eine Kugel. Mit welcher Wahrscheinlichkeit...
- a) zieht er die Kugel mit der Zahl 12?
- b) zieht er eine Zahl, die durch 3 teilbar ist?
- c) zieht er eine Zahl, die größer als 11 ist?
- d) zieht er eine Quadratzahl?
Schreibe für jede Teilaufgabe die passenden Ereignismengen auf.
Es handelt sich um ein Laplace-Experiment, da jede Kugel mit der gleichen Wahrscheinlichkeit gezogen wird. Es gibt insgesamt 20 mögliche Ergebnisse bei der Ziehung
- a) Die Ereignismenge ist: A = {12}
- In der Ereignismenge ist also ein günstiges Ergebnis =>
- b) Die Ereignismenge ist: B = {3, 6, 9, 12, 15, 18}
- In der Ereignismenge sind also sechs günstige Ergebnisse =>
- c) Die Ereignismenge ist: C = {12, 13, 14, 15, 16, 17, 18, 19, 20}
- In der Ereignismenge sind also neun günstige Ergebnisse =>
- d) Die Ereignismenge ist: D = {1, 4, 9, 16}
- In der Ereignismenge sind also vier günstige Ergebnisse =>
Du siehst hier zwei Glücksräder
- a) Du gewinnst, wenn das Glücksrad auf der Farbe Grün landet.
- Bei welchem ist die Gewinnchance höher? Begründe deine Antwort!
- b) Wie wahrscheinlich ist es beim Glücksrad 1 einen Sektor zu bekommen, der neben einem grünen Sektor liegt?
- c) Wieviele rote Sektoren müsste Glücksrad 2 haben, damit die Wahrscheinlichkeit für einen roten Sektor bei 75% liegt?
- a) Es ist besser sich für das 1. Glücksrad zu entscheiden, da es dort wahrscheinlicher ist auf grün zu landen.
Denn es gilt für das 1. Glücksrad: Es gibt insgesamt 6 gleichgroße Sektoren und 2 davon sind grün. Daher gilt für die Gewinnwahrscheinlichkeit:
- P(A) =
Für das 2. Glücksrad gilt: Es gibt insgesamt 8 gleichgroße Sektoren und 2 davon sind grün. Daher gilt für die Gewinnwahrscheinlichkeit:
- P(B) =
- b) Es gibt insgesamt 4 Sektoren aus den 6 Sektoren, die neben einem grünem Sektor liegen. Daher gilt:
- P("neben grün") =
- c) Wir müssen die Anzahl x berechnen, um die Wahrscheinlichkeit für 75% zu bestimmen:
Du siehst folgendes Glücksrad
Es werden folgende Regeln zum Gewinnen angeboten:
- a) Du gewinnst bei einer Zahl die durch 3 teilbar ist
- b) Du gewinnst bei rot und einer geraden Zahl
- c) Du gewinnst bei grün oder blau
- d) Du gewinnst bei 4, 5, 6
- Für welche Regel entscheidest du dich, um zu gewinnen? Begründe deine Antwort.
Um zu entscheiden, welche Gewinnregel die größte Chance hat zu gewinnen, sollte man die Wahrscheinlichkeiten zu den einzelnen Ereignissen der Regeln bestimmen:
P(A) = = 0,333
P(B) = = 0,083
P(C) = = 0,417
P(D) = = 0,25
Man sollte sich für die Regel c) entscheiden, da die Wahrscheinlichkeit zu gewinnen dort am größten ist.
Du hast zwei Möglichkeiten dich für ein Gewinnspiel zu entscheiden:
- 1) Entweder du ziehst aus der folgenden Urne und gewinnst bei der Farbe gelb oder blau
- 2) Oder du Würfelst einen sechsseitigen Würfel und gewinnst bei den Zahlen kleiner als 3
Für welches Gewinnspiel entscheidest du dich? Berechne zur Begründung deiner Etscheidung die Gewinnwahrscheinlichkeiten der Spiele aus.
Man sollte sich für das Urne in dem Gewinnspiel entscheiden, da es dort wahrscheinlicher zu gewinnen.
Die Urne hat insgesamt 13 Kugeln, darunter sind 3 gelbe und 2 blaue Kugeln.
P("Urne") = = 0,385
Ein Würfel hat Sechs mögliche Ergebnisse, darunter ist einmal die Augenzahl 2 und einmal die Augenzahl 1. Daher gilt für die Gewinnwahrscheinlichkeit:
P("Würfel") = = 0,33
Ein Kartenspiel hat 32 Karten mit den vier Farben: Herz, Karo, Pik und Kreuz. In jeder Farbe gibt es jeweils die Karten 7, 8, 9, 10, Bube, Dame, König und Ass.
Wie hoch ist die Wahrscheinlichkeit für folgende Ereignisse:
- a) Es wird eine Karte der Farbe Karo gezogen?
- b) Es wird eine Dame gezogen?
- c) Es wird nicht eine schwarze 10 gezogen?
- d) Es wird keine Bildkarte gezogen?
Lösung für a):
In dem Kartendeck gibt es insgesamt 32 Karten, wovon 8 Karten der Farbe Karo angehören. Daher folgt:
P("Karo-Karte wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 25% eine Karo-Karte gezogen.
Lösung für b):
Es gibt 4 Damen in einem Kartendeck, daher gilt:
P("Dame wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 12,5% eine Dame gezogen.
Lösung für c):
Es gibt zwei schwarze 10 in Deck (Pik und Kreuz), daher folgt:
P("schwarze 10 wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 6,25% eine schwarze 10 gezogen.
Lösung für d):
Hier soll KEINE Bildkarte gezogen werden, man muss also die Anzahl der Karten zählen, die keine Bildkarten sind. Die 7,8,9,10 sind keine Bildkarten und von jeder Karte gibt es durch die unterschiedlichen Farben 4 Stück. Es gibt also insgesamt 16 Karten im Deck, die nicht zu den Bildkarten zählen, daher folgt:
P("keine Bildkarte wird gezogen") =
Es wird also mit einer Wahrscheinlichkeit von 50% keine Bildkarte gezogen.
Zu sehen ist eine Urne, die noch keine Kugeln enthält.
Befülle für jede Teilaufgabe eine Urne so (selber skizzieren), dass folgende Wahrscheinlichkeiten eintreten:
Die Grundmenge der Kugeln kann bei jeder Teilaufgabe frei gewählt werden.
- a) Die Wahrscheinlichkeit eine blaue Kugel zu ziehen ist P("blaue Kugel") = 0,25.
- b) Die Wahrscheinlichkeit eine rote Kugel zu ziehen ist P("rote Kugel") = 0,10.
- c) Die Wahrscheinlichkeit eine grüne Kugel zu ziehen ist P("grüne Kugel") = 0,15.
- d) Die Wahrscheinlichkeit eine gelbe Kugel zu ziehen ist P("gelbe Kugel") = 0,50.
- e) alle Wahrscheinlichkeiten aus a), b), c), d) sollen gleichzeitig eintreffen
Es ist einfacher sich zunächst über eine geeignete Menge an Kugeln in der Urne Gedanken zu machen.
Hier sind geeignte Mengen an Kugeln in der Urne, um die Aufgabe gut lösen zu können.
- a) 4
- b) 10
- c) 20
- d) 2
- e) 20
Jetzt müsst ihr nur überlegen, wie ihr die Kugeln einfärben müsst.
- a) z.B. bei 1 blaue Kugel und 3 Kugeln anderer Farbe.
- b) z.B. 1 rote Kugel und 9 Kugeln anderer Farbe.
- c) z.B. 3 grüne Kugel und 17 Kugeln anderer Farbe.
- d) z.B. 1 gelbe Kugel und 1 Kugel anderer Farbe.
- e) z.B. 10 gelbe Kugeln, 3 grüne Kugeln, 2 rote Kugeln und 5 blaue Kugeln.