Experimentierkasten zur Binomial- und Normalverteilung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
|||
| Zeile 15: | Zeile 15: | ||
<small>Ansicht der GEOGEBRA-Anwendung</small> | <small>Ansicht der GEOGEBRA-Anwendung</small> | ||
< | |||
<ggb_applet height="650" width="800" filename="Binomialverteilung.ggb" /> | |||
<br> | |||
<small>'''Erklärungen'''<br> | <small>'''Erklärungen'''<br> | ||
| Zeile 115: | Zeile 123: | ||
*[http://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm Rechner für Normal- Bionomial- und Poissonverteilung] | *[http://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm Rechner für Normal- Bionomial- und Poissonverteilung] | ||
<br> | <br> | ||
<center> | <center></center> | ||
</center> | |||
Version vom 24. Februar 2018, 15:36 Uhr
Die Binomialverteilung und Wahrscheinlichkeiten binomial verteilter Größen
Für die Binomialverteilung gelten bekanntlich folgende wichtige Formeln:

Sie spielen eine wichtige Rolle bei den Tests binomial verteilter Größen. In der Regel kommt man dabei nicht ohne eine Stochastische Tabelle aus.
Mittels Geogebra sollen nun diese Berechnungen wie mit einem Computer-Algebra-System durchgeführt. Neben den reinen Berechnungen ergibt sich auch ein besseres Verständnis mancher Zusammenhänge.
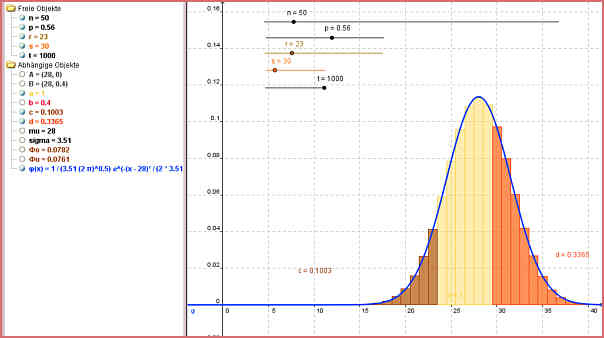
Ansicht der GEOGEBRA-Anwendung

Erklärungen
1. Geogebra läuft nur mit dem Geometriefenster innerhalb des Wikis. Um die volle Funktionalität von Geogebra zur Verfügung zu haben (hier das Algebra-Fenster) mit Doppelklick ins Geometriefenster und die entsprechende Datei öffnet sich mit der auf ihrem Rechner installierten Geogebraversion.
2. Erklärung der Regeler und Variablen im Algebra-Fenster: ./.
Wahrscheinlichkeiten bestimmen
Die B(n,p,r)-Werte liest man im Geometrie-Fenster ab. Um die F(n,p,r), also die aufsummierten Wahrscheinlichkeiten bis r zu erhalten, aktiviert man den Knopf c und variiert den Schieberegler r. Eine ähnliche Funktion hat der Knopf d mit dem Schieberegler s, die Wahrscheinlichkeiten ab s bis n aufsummiert. Die Werte liest man im Algebrafenster ab. Einstellungen für die Genauigkeit, maximalem n, r, s nach Bedarf ändern.
4. Bestimme mittels des der Geo-Gebra-Datei
....a)P(Z = k) für p = 0,5 n = 1000 k = 400; p = 0,8 n = 50 k = 40
....b)P(Z <=k) für p = 0,4 n = 500 k = 350; p = 0,6 n = 100 k = 55
....c)P(Z >=k) für p = 0,25 n = 200 k = 75; p = 0,2 n = 500 k = 70
....d)P(k1<=Z<=k2) für p= 0,4 n = 200 k1= 60; k2 = 100
Vergleiche die Werte mit Taschenrechnerwerten bzw. Werten aus der Tabelle.
Beispiel für eine Fragestellung, die mit Tabelle nicht lösbar ist:
In einem Biotop treten zwei Varietäten der gleichen Art auf, die sich äußerlich nicht unterscheiden: Varietät A mit einer Wahrscheinlichkeit von 40 %, Varietät B mit einer Wahrscheinlichkeit von 60 %. Unter der Annahme die beiden Varietäten seien in dem Biotop binomial verteilt sollen nun für weitere Untersuchungen eine bestimmte Anzahl n von der Art gefangen werden:
a) Wie groß ist n zu wählen, damit man mit 80-%-iger Wahrscheinlichkeit mindestens 1 Exemplar der Varietät A fängt.
b) Wie groß ist n zu wählen, damit man mit 80-%-iger Wahrscheinlichkeit mindestens 50 Exemplare der Varietät A fängt.
Lösung Aufgabe a)
Über das Gegenereignis erhält man: ![]()
Mittels der festen Einstellung p = 0,4 und s = 1 erhält man mittels Experimentieren mit dem Schieberegler n die Lösung n = 4
Lösung Aufgabe b)
Die Aufgabe ist mit der Binomialverteilung rechnerisch nicht lösbar. Auch die Stochastische Tabelle liefert keine Lösung, da Die F(n,p,r) über n tabelliert sind, aber nicht über r.
Die Aufgabe mit dem "Experimentierkasten" für festeingestelltes p = 0,4 und s = 50 liefert n = 136.
Testverfahren für binomial verteilte Größen
|
Arbeitsaufgaben: Einseitiger Hypothesentest 1. Sieh das Video genau an. Es hat sich ein Fehler eingeschlichen. Entdeckst Du ihn?
|
Links



